Trees

Setting up the environment

We’ll now use NLTK to do a little bit of actual theoretical linguistics. This is at least partly based on chapter 8 of the NLTK book.

The first step is to get the environment set up. Because we want to save a file and have Python find it, we need to put the files someplace it looks.

I mainly know how to do this on a Mac—if you are working in Windows, something similar should be possible.

It turns out that the Python console (iPython console) in Spyder will accept some commands that let you change your “working directory.” If you type

pwd

(for “print working directory”), it should tell you where it will look for files. When I did that just now it told me /Users/hagstrom (because my user name on this computer is hagstrom, so this is my home directory). If you do not see something analogous when you try this, you can point the working directory at somewhere else using cd like this:

cd /Users/hagstrom

(for “change directory”). After doing that, pwd should tell you it’s now looking where you just pointed it to. Although I don’t have a means to test it, my guess is that on Windows you can use the same thing except with backslashes (\) instead of forward slashes (/). That is, I think the Windows home directory is \Users\username\.

Just to make sure everything’s working, though, let’s start with this, which kind of mimics what we were trying to in class.

Create a new file (choose New File… from the File menu in Spyder), and the clean out the template stuff it puts in there (like “# -*- coding: utf-8 -*-” etc.) so that it is actually empty.

Type just the following:

S -> NP VP

And save. It will bring up a file dialog, and it would normally insist that you save it as a file ending in .py—but we want to save this as a file ending in .cfg (“context-free grammar”). On the Mac at least, in order to make it allow a .cfg file extension, you need to select the popup that says “Files of type:” and change it to “All files (*)” first. Then it will let you save a .cfg file. Save it as something like homework4.cfg in your home directory (or, wherever you pointed your working directory at).

If it worked, you should be able to do the following without getting any errors (or, indeed, any kind of response).

import nltk
hw4cfg = nltk.data.load("file:homework4.cfg")

If you did get errors, it probably could not find the file, which would mean either it is looking in the wrong folder, or you saved it in the wrong folder, or both. Or there’s just a typo. To be sure it worked (in the absence of any response), try:

>>> hw4cfg.productions()
[S -> NP VP]

It should give you the rule you entered into homework4.cfg.

Next, add two more lines to homework4.cfg so that it looks like this:

S -> NP VP
NP -> "I"
VP -> "left"

and save it. Now, we’ll re-load it. Before we loaded it like in the block below—but if you try that now, you’ll find that it didn’t update hw4cfg:

>>> hw4cfg = nltk.data.load("file:homework4.cfg")
>>> hw4cfg.productions()
[S -> NP VP]

The reason (as I mentioned quickly in class) is that NLTK believes it already loaded this, so it doesn’t bother to load it again. We need to explicitly tell it that it needs to read the grammar again. The way we do that is to give it a cache=False parameter, to tell it not to read from its “cache” of stored files, but to read it in from the disk again.

>>> hw4cfg = nltk.data.load("file:homework4.cfg", cache=False)
>>> hw4cfg.productions()
[S -> NP VP, NP -> 'I', VP -> 'left']

That’s more like it. So, don’t forget about this as you change your grammar, you need to tell NLTK explicitly that you need it to be re-loaded.

Last bit of setup, let’s get it to draw a simple tree with this grammar. Clearly, this grammar is only useful for parsing the sentence “I left.” So, we will set that up. We set raw to be the string of words representing the sentence. We then split it into words (a form of “tokenizing”) using split() (which breaks raw at the spaces). The print(sent) line is there so you can see what it did. We then ask NLTK to make us a recursive descent parser based on the hw4cfg grammar, which we will call parser.

raw = "I left"
sent = raw.split()
print(sent)
parser = nltk.RecursiveDescentParser(hw4cfg)
treegen = parser.parse(sent)
trees = [t for t in treegen]
print(trees)
trees[0].draw()

Once we had parser set up, we asked the parser to parse our sentence, and store the result in treegen. I used this name because what we have really at this point is not the possible trees for the sentence, but rather a generator of those trees. The next step (trees = [t for t in treegen]) actually makes a list of those trees. It might seem like that line does very little, but it forces NLTK to use the treegen generator to construct the trees and put them in a list, called trees. Now we actually have a list of trees. The print(trees) shows you that. Then the last line tells the first (and in this case, only) tree in trees to draw itself.

When you say trees[0].draw(), this will cause a program (also called python, just like Spyder is) to start, and display a window with a small tree in it. This window is likely going to be hidden behind the Spyder window. You’ll need to find it, look at the tree it drew, and then explicitly close it—only then will you get control back in the console.

I hope that at this point, everything has either gone smoothly or at least been troubleshootable enough that we can proceed to do actual things from here on.

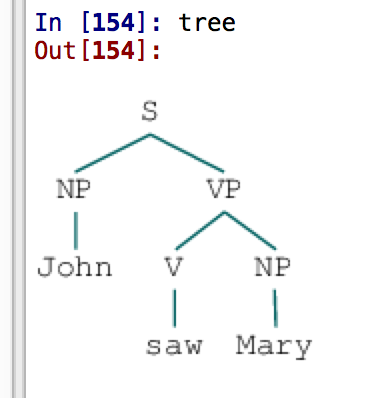
Developing a phrase structure grammar

We can start with the basic “park grammar” that we used in class (and which comes from the book).

So, you can fix up homework4.cfg to have the rest of this grammar in it. It should be evident that this grammar can handle sentences like “Mary saw Bob,” “my dog saw a cat in the park,” “a dog ate John.”

S -> NP VP
VP -> V NP | V NP PP
PP -> P NP
V -> "saw" | "ate" | "walked"
NP -> "John" | "Mary" | "Bob" | Det N | Det N PP
Det -> "a" | "an" | "the" | "my"
N -> "man" | "dog" | "cat" | "telescope" | "park"
P -> "in" | "on" | "by" | "with"

Task 1. Prove to yourself that this can indeed handle “Mary saw Bob,” “my dog saw a cat in the park,” and “a dog ate John” by following the procedure we used above for “I left.”

Task 2. Add adjectives to the grammar so that it can handle “My annoying little dog saw a cat in the lovely park” and “a vicious dog ate John.”

Task 3. This grammar will give you nothing for “a man walked in the park”. Why?

If you haven’t done this already, let’s define a function that can take a string, break it up into words, parse it, and return the trees. That will make it simpler to deal with things. What I had in mind is a function like this:

def get_trees(raw):
    sent = raw.split()
    hw4cfg = nltk.data.load("file:homework4.cfg", cache=False)
    parser = nltk.RecursiveDescentParser(hw4cfg)
    treegen = parser.parse(sent)
    trees = [t for t in treegen]
    return trees

This will re-initialize the parser each time, as well, so we don’t need to keep doing those steps by hand as we change things. Once we have that defined, we can just say:

>>> trees = get_trees("a man walked in the park")
>>> trees
[]
>>> trees = get_trees("John saw Mary")
>>> trees
[Tree('S', [Tree('NP', ['John']), Tree('VP', [Tree('V', ['saw']), Tree('NP', ['Mary'])])])]

Next, we will try to find the subject of a sentence. Descriptively, the subject of a sentence is the NP that is a daughter of S. Ultimately, in this grammar we have built so far, it’s always going to be in the same place, but let’s explore this a little bit anyway.

We can take a tree that our parser has found for us and break it up into subtrees, which will allow us to isolate NP-daughter-of-S pretty easily. So, for the “John saw Mary” tree, what get_trees("John saw Mary") gives us back is a list of parses (containing just one element), so let’s look at that tree. We’ll name it tree:

>>> tree = get_trees("John saw Mary")[0]
>>> print(tree)
(S (NP John) (VP (V saw) (NP Mary)))

If you ask a Tree to give you subtrees() it will go through a tree and give you a list of all the subtrees contained in it.

>>> [s for s in tree.subtrees()]
[Tree('S', [Tree('NP', ['John']), Tree('VP', [Tree('V', ['saw']), Tree('NP', ['Mary'])])]),
 Tree('NP', ['John']),
 Tree('VP', [Tree('V', ['saw']), Tree('NP', ['Mary'])]),
 Tree('V', ['saw']),
 Tree('NP', ['Mary'])]

So, if we want to find the “NP daughter of S”, we look for a subtree whose label is “S” and for which the label of one of the contained Tree nodes is “NP”.

There are not many subtrees that have the label “S”. In fact, there’s just the one, and it’s the whole tree. But we can still find it in a more general way, by adding an if clause to the list comprehension we used to display them above.

>>> [s for s in tree.subtrees() if s.label() == "S"]
[Tree('S', [Tree('NP', ['John']), Tree('VP', [Tree('V', ['saw']), Tree('NP', ['Mary'])])])]

Now, we want to find the daughter of that node S whose label is “NP”. What are the daughters of S? A Tree basically behaves like a list, so we can count the number of daughters with len(tree) and go through them with for n in tree. If there are two, tree[0] will be the left one, and tree[1] will be the right one.

This is illustrated below. Notice that at the end, when we are looking at the left daughter of VP, we can address it in three equivalent ways: we can explicitly request the 0th element of the 1st element of the snode Tree (that is, the left daughter of the right daughter of S), or we can compress that into a tuple and ask for the (1, 0)th element (still means the left daughter of the right daughter of S), and it’s possible (though kind of confusing I think) to leave the parentheses off the tuple when it is within square brackets (like in the last example).

>>> snodes = [s for s in tree.subtrees() if s.label() == "S"]
>>> snode = snodes[0]
>>> print(snode)
(S (NP John) (VP (V saw) (NP Mary)))
>>> len(snode)
2
>>> print(snode[0])
(NP John)
>>> len(snode[0])
1
>>> print(snode[1])
(VP (V saw) (NP Mary))
>>> len(snode[1])
2
>>> print(snode[1][0])
(V saw)
>>> print(snode[(1,0)])
(V saw)
>>> print(snode[1,0])
(V saw)

So, this is how you navigate subtrees. If we have snode set to be an “S”-labeled Tree, as we did above, we can cycle through its daughters and find the one that has an “NP” label, and that will be the NP daughter of S.

>>> [d for d in snode if d.label() == "NP"]
[Tree('NP', ['John'])]

We can actually combine these in a single (though complicated) list comprehension. This takes the NP-finder above, but adds in the computation of snodes as well. Notice the order. We’re making a list of ds, which are the daughters of snode. So we continue to start with [d for... but then we are going to find the snodes first, and then the daughters of those once we have an snode. So, we continue with n in tree.subtrees() if n.label() == "S" meaning that n is going to be a subtree with label “S” that we want to then check the daughters of. So, then we go through the daughters with for d in n if d.label() == "NP". Put together, it looks like this:

[d for n in tree.subtrees() if n.label() == 'S' for d in n if d.label() == 'NP']

Task 4. Understand how that complex list comprehension works. Convince yourself by changing it to find the object. (What we did above is find the subject, which is the NP daughter of S. So, how do we characterize the object? Use the technique above to find it. The answer should be “Mary”, right?)

Now, let’s enhance the grammar by adding the ability to embed clauses, like in “Bob thought that John saw Mary” and “Bob said that John saw Mary”.

Task 5. Enhance the grammar so that it can parse “Bob thought that John saw Mary” and “Bob said that John saw Mary”.

Task 6. Give trees for “Bob said that John saw Mary in the park” and “the annoying man thought that Bob said that my dog saw a vicious cat in the park”. Ideally, drawn out using tree.draw() but you can give the print(tree) version too.

Task 7. Find the subjects of those sentences using our subject-finding procedure from before. (Should be “Bob” and “John” in one case, “the annoying man”, “Bob”, and “my dog” in the other.)

Task 8. Find the objects of those sentences using our object-finding procedure from before. (Should be “Mary” in one case, “a vicious cat (in the park)” in the other.)

Relative clauses

A relative clause is something like “who saw Mary” in “the man who saw Mary”. It is formed by adding a wh-question to a noun, more or less. So the referent of “the man who saw Mary” is the individual that is a man, and also the answer to the question “Who saw Mary?”.

Suppose we want our parser to recognize “the man who saw Mary” as an NP.

It can already recognize “the man” and “the man in the park”, so we can simply add an extra option for the NP rule to allow for this.

Task 9. If we just add ... | Det Nom S | "who" to the NP rule, we can parse “the man who saw Mary saw Bob”. Give some reasons why this is not really that good a solution.

Coming up with a better solution though is kind of difficult. Let’s see if we can hammer together a kind of a solution for this case before we look at the more general problem.

In “the man who saw Mary”, it seems like “who” is basically the subject of “saw”. So, “who saw Mary” is a special kind of sentence with “who” as the subject. Let’s define this kind of special case by, first, making “who” a special kind of NP, and then making a relative clause be a special kind of sentence with “who” as its subject.

That is, add the following to the grammar:

RP -> "who"
RC -> RP VP
NP -> Det Nom RC

Task 10. Draw a tree using the grammar above of “the man who saw Mary saw Bob”.

There’s another form a relative clause can take, though. You can also say “the man who Mary saw saw Bob”. What’s different here is that “who” is now really playing the role of the object of the “saw” that Mary did. But “who Mary saw” is not in the right form for parsing.

What’s going on? Well, the relative pronoun “who” generally corresponds to a gap in the sentence. We didn’t notice the gap in subject posistion, but it’s obvious when the gap is in the object position. These relative clauses are, again, basically wh-questions, and the normal way wh-questions are formed is to move the wh-word to the front of the clause.

And this is where parsing becomes difficult, when things move around in a sentence.

Let’s try a kind of a hack to make this work.

For any transitive verb (“saw”, “ate”, and “walked” in our grammar), there is the version we already have, which form a VP with their object NP. If any of these appear in an “object relative”, then the object NP will be missing. So, let’s make a version of the VP that has a gap. That is, let’s define VPG to be just V rather than V NP.

Task 11. Define VPG that way in the grammar, so that any VP has an analogous VPG without an object.

We haven’t used VPG yet in the grammar apart from defining it. But conceptually, what we want is that VPG should be available in a relative clause where the object is missing. So, we want to redefine RC, in a form that’s closer to what we believe the structure of these is. So replace the RC definition you added before with this:

RC -> RP SOG
SOG -> NP VPG

The idea here is that SOG (sentence-with-object-gap) is like a regular S but has a VP with an object gap.

Task 12. Draw a tree using the grammar we have at this point of “the man who Mary saw in the park saw Bob”.

VP -> V NP | V NP PP

Doing this broke our ability to parse the subject relative “the man who saw Mary”, however.

With our new understanding of relative clauses, the gap in “the man who saw Mary” must actually be the subject of “saw”. So, let’s add some rules to get subject relatives as well.

Start by adding RC -> RP SSG to the grammar (SSG being intended to mean “sentence-with-subject-gap”). So, there are now two kinds of relative clause the grammar can handle. Both start with the RP “who”, and one continues with SSG (an S but missing the subject), and the other continues with a SOG (an S but missing the object). We still need to define SSG. What should it be?

Task 13. Add a definition of SSG into the grammar.

Now we should be able to parse both “the man who saw Mary saw Bob” and “the man who Mary saw saw Bob”.

Task 14. Draw trees of “Mary walked the dog who my cat saw in the park” and “Mary walked the dog who saw my cat in the park”.

There were other things I was thinking about trying out here, but this is good enough.